
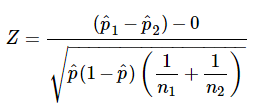
We need to conduct a hypothesis test on the claimed cancer rate.Explain why the significance level should be so low in terms of a Type I error. Hypothesis Testing: Two Means, Paired Data, Two Proportions 10.1 Hypothesis Testing: Two Population Means and Two Population Proportions1 10.1.1 Student Learning Objectives By the end of this chapter, the student should be able to: Classify hypothesis tests by type. Since this is a critical issue, use a 0.005 significance level. Test the claim that cell phone users developed brain cancer at a greater rate than that for non-cell phone users (the rate of brain cancer for non-cell phone users is 0.0340%). In a study of 420,019 cell phone users, 172 of the subjects developed brain cancer. In reality, one would probably do more tests by giving the dog another bath after the fleas have had a chance to return. The alternative hypothesis, \(H_\) is very close to alpha.For this reason, we call the hypothesis test left, right, or two tailed. When you calculate the \(p\)-value and draw the picture, the \(p\)-value is the area in the left tail, the right tail, or split evenly between the two tails.If no level of significance is given, a common standard to use is \(\alpha = 0.05\).

The statistician setting up the hypothesis test selects the value of α to use before collecting the sample data.In a hypothesis test problem, you may see words such as "the level of significance is 1%." The "1%" is the preconceived or preset \(\alpha\).


 0 kommentar(er)
0 kommentar(er)
